Phylogenetic analysis

1. To classify living species of organisms : Modern classification is based on molecular phylogenetic analysis in which the characters are aligned nucleotide or amino acid sequences. Closely related organisms generally have a high degree of agreement in the molecular structure of these substances, whereas the molecules of organisms distantly related usually show a pattern of dissimilarity. Molecular phylogeny uses such data to build a "relationship tree" that shows the probable evolution of various organisms, which is the basis of species classification.
2. To apply to genetic testing and forensics: Phylogenetics has been applied to the very limited field of human genetics, such as genetic testing to determine a child's paternity as well as the criminal forensics focused on genetic evidence.
3. To infer functions of new genes: Phylogenetic analysis can be used to examine whether a new gene is related to another well-characterized gene in another species to infer the potential functions of that new gene. Phylogenetic analyses are increasingly being performed on a genomic scale to predict gene and protein functions.

The steps involved in phylogenetic analysis :

1. Collecting data :

The data subjected to the phylogenetic analysis are homologous, that is, related by evolutionary descent. Among many methods is' the sequence-similarity searching method, which can be used to retrieve homologous sequences. This tool can be accessed at sites such as the National Centre of Biological Information (http://www.ncbi.nlm.nih.gov), the Japanese GenomicNet server (http://www.blast/genome.ad.jp), and the European Bioinformatics Institute (http://www.ebi.ac.uk). The starting point of a phylogenetic analysis is usually a set of related proteins because it is more informative to work with proteins; more distant relationships can be analyzed.

2. Multiple sequence alignments

Once a set of sequences to be subjected to the phylogenetic analysis is collected, the next step is to perform a multiple sequence alignment.

3. Building the phylogenetic tree :

Once the sequences have been aligned, the multiple alignment file becomes the input for a phylogenetic analysis program. Numerous phylogenetic methods have been proposed, because no single method performs well in all situations.
There are three major types of methods:

1. distance matrix,
2. maximum parsimony,  
3. maximum likelihood.

In distance matrix methods, the number of nucleotide or amino acid substitutions between sequences is treated as a distance and computed for all pairs of taxa. The phylogenetic tree is constructed based on these distances.

Neighbour-joining, one of commonly applied distance methods, is statistically consistent under many models of evolution, and hence capable of reconstructing the true tree with high probability. Distance methods are quick to compute. A central idea of the maximum parsimony is that the preferred evolutionary tree requires the smallest number of evolutionary changes to explain the differences observed among the taxa under study. Although parsimony makes no explicit assumptions, there is the critical assumption of the parsimony criterion that a tree requiring fewer substitutions or changes is better than a tree requiring more. This can be contrasted with likelihood methods, which make explicit assumptions about the rate of evolution and patterns of nucleotide substitution. Maximum parsimony is a very simple approach, and is popular for this reason. However, it is not statistically consistent; that is, it is not guaranteed to produce the true tree with high probability, given sufficient data. Maximum parsimony methods take longer to compute. Maximum likelihood method is a popular statistical method used to make inferences about parameters of the underlying probability distribution of a given data set. Maximum likelihood methods are very slow, typically computer intensive, and have not been implemented as widely as other methods.

There are two main kinds of information inherent in any phylogenetic tree:

The topology of a tree defines the relationships of the proteins (or other objects) that are represented in the tree.

For example, the topology shows the common ancestor of two homologous protein sequences.

The branch lengths sometimes (but not always) reflect the degree of relatedness of the objects in the tree.

A phylogenetic tree is a graph composed of branches and nodes.

Only one branch (also called an edge) connects any two nodes.

The nodes represent the taxonomic units (taxa or taxons); the node (from the Latin for "knot") is the intersection or terminating point of two or more branches.

An internal node is bifurcating if it has only two immediate descendant lineages (branches).

Bifurcating trees are also called binary or dichotomous; any branch that divides splits into two daughter branches.

A tree is multifurcating if it has a node with more than two immediate descendants.
An operational taxonomic unit (OTU) is an extant taxon present at an external node or leaf; the OTUs are the available nucleic acid or protein sequences that we are analyzing in a tree. The internal nodes represent ancestral sequences that we can infer but can only very rarely observe. Some OTUs can be swapped (that is, rotated or exchanged) without altering the topology of the tree.
Branches define the topology of the tree, that is, the relationships among the taxa in terms of ancestry. Branch lengths should be defined for every tree. In some trees, the branch length represents the number of nucleotide or amino acid changes that have occurred in that branch.

A phylogram has the helpful feature of conveying a clear visual idea of the relatedness of different proteins within the tree.

In a cladogram the branches are unsealed i.e. they are not proportional to the number of changes.

This type of tree has the advantage of aligning the OTUs neatly in a vertical column. This may be especially useful if the tree has many dozens of OTUs.

A clade is a group of all the taxa that have been derived from a common ancestor plus the common ancestor itself. A clade is also called a monophyletic group.
A phylogenetic tree can have a root representing the most recent common ancestor of all the sequences. If one assumes a constant molecular clock, then time and distance are proportional: the direction of time moves from oldest (at the root) to newest (at the OTUs). Often the root is not known, and some tree making algorithms do not provide conjectures about placement of a root. The alternative to a rooted tree is an unrooted tree An unrooted tree specifies the relationships among the OTUs. However, it does not define the evolutionary path completely or make assumptions about common ancestors. If a tree is unrooted you may choose to add a root. The two main ways to do this are by specifying an outgroup and by midpoint rooting. To specify an outgroup, one or more sequences that are known to have diverged earlier than the restare included in the dataset.
The number of possible trees to describe the relationships of a dozen protein sequences is staggeringly large. There is only one "true" tree representing the evolutionary path by which molecular sequences (or even species) evolved.

The number of potential trees is useful in deciding the tree-making algorithms to apply.
Expert Protein Analysis , System (ExPASY) proteomics tools (http://ca.expasy.0rg/tools/#phylo) has, under the heading "Phylogenetic Analysis," a fairly comprehensive collection of phylogenetic analysis programs.
There, nearly 300 phylogenetic analysis programs and servers are listed. Many of those listed programs are available on the Web, including both free and non-free ones. The software programs are conveniently categorized by methods available, by computer systems on which they work, and the particular types of data analysed.

4. Tree evaluation :

After a phylogenetic tree is built, it is necessary to evaluate it for robustness. The most common method for doing this is bootstrap analysis, which essentially involves resampling the database and then analysing the resampled data. Those robust results obtained from initial phylogenetic analysis will tolerate variations introduced by the resampling process, whereas nonrobust results will be altered and yield different trees when small changes in data are made through resampling.

 

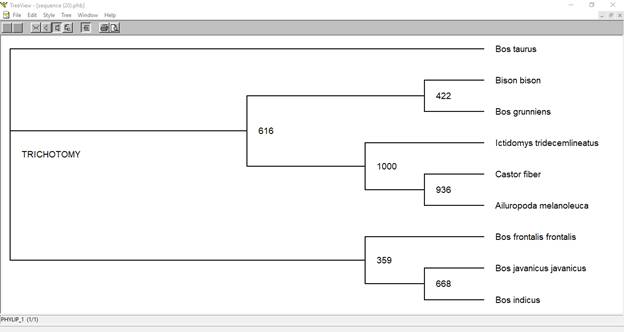
5. Tree visualization :

After robust trees are created, the final step is to best visualize trees and produce publication-quality printouts of the results.

The following experiment will be carried out using ClustalX for multiple sequence alignment followed by phylogenetic analysis. The ClustalX program is by far the most commonly used program for making multiple sequence alignments, it was first described by Paula Hogeweg in the early 80's and was later developed by Desliggins.
ClustalX is a fully automatic program for global multiple alignment of DNA and protein sequences which works on the hypothesis that sequences in an alignment will repeat their evolutionary history. The alignment is progressive and considers sequence redundancy. Trees can also be calculated from multiple alignments. The program has some adjustable parameters with reasonable defaults. The program
follows the following steps :

• Performs pairwise alignment of all the sequences.
• Uses the alignment score to give a phylogenetic tree using the neighbor-joining method.
• Sequences are aligned using phylogenetic relationship indicated by a tree.

Produces best match for selected sequences and arranges them so that the identities, similarities and differences can be seen simultaneously.

Evolutionary relationships can be studied using cladograms.
In this experiment we will look at the evolutionary relationships of animals as indicated by sequence differences in cytochrome c oxidase subunit I. This is encoded in the mitochondrial genome and has been proposed as a "barcode" for identifying animal species. Two of the sequences downloaded will also be used for pairwise sequence alignment using BLAST. We will use a web browser to find sequences, which we will copy back to our PC and analyze using two widely-used programs that run in Windows: ClustalX to align the sequences and calculate a tree by the Neighbor-Joining method (which is based on a distance matrix), and then TreeView to display and manipulate the tree into a form suitable for publication.